Projectile motion (Motion on 2D)
Projectile motion (Motion on 2D) air resistance neglected
When the velocity and acceleration of the body acts except and consists of projectile motion.
During projectile motion horizontal velocity and total energy remains same.
Two types of projection are considered in the chapter:
(i) Oblique projection
(ii) Horizontal projection from height
i. Oblique projection
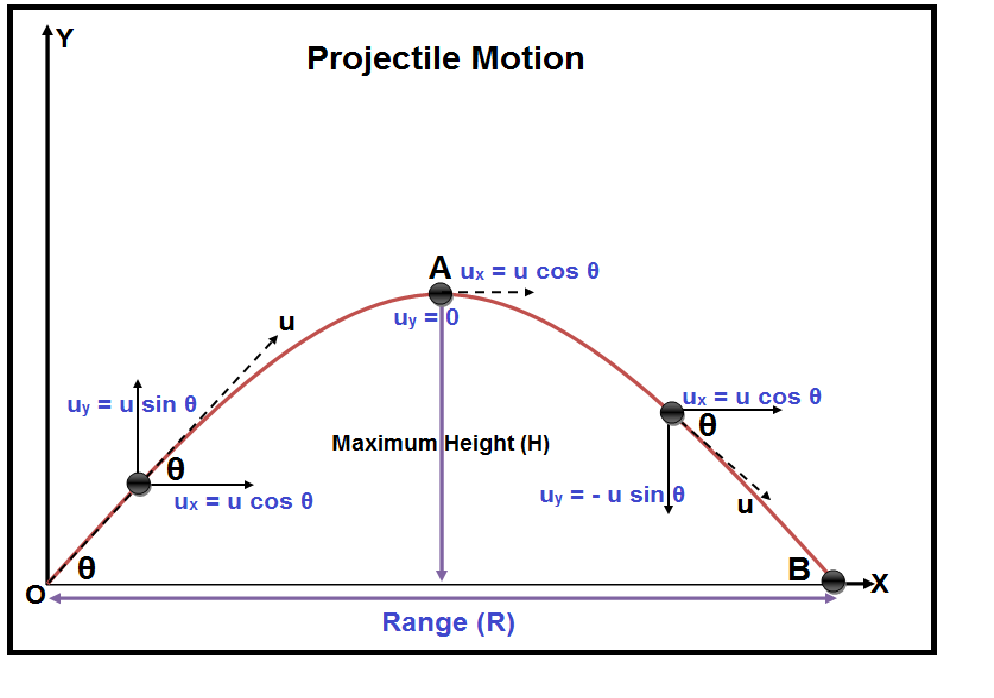
Time of projectile
total vertical height=0
Using equation of motion on straight line
or,
or,
so time to reach maximum height =
Maximum height
Maximum height during the journey of projectile.
At maximum height : vertical velocity=0, horizontal velocity=
Using equation of motion on 1D ( vertical direction)
so,
Range of projectile
It is the horizontal distance travelled by the projectile.
Range(R)= Horizontal distance * time taken
or,
or,
or, ...........(iii)
For maximum range ,
For angles and (90-) has the same range.
Equation of trajectory
Let x be the horizontal distance travelled at any time t, then,
Then vertical distance corresponding to horizontal distance x is
which is on the form , is parabolic.
where, and
Range(R)=
Maximum height=
Dividing equation (ii) and (iii)
Velocity after certain time t is:
Horizontal velocity= constant=
Vertical velocity=
so, the net velocity v after time t is
and the angel made by the velocity is
Energy during projectile motion
Initially, Total energy=Kinetic energy=
During motion at highest point
K.E.==
P.E.=mgh=mg=
T.E. = K.E. + P.E. ==
Hence total energy of projectile is conserved.
similarly, energy could be find out at other time.
Horizontal projection from height
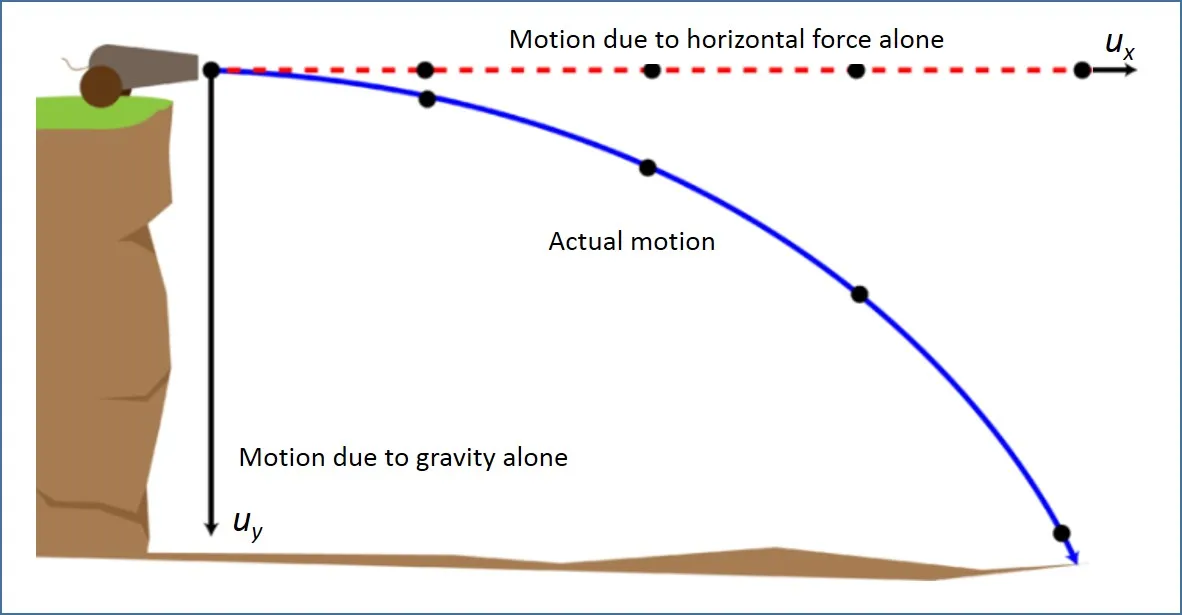
At time t, horizontal distance travelled x=u*t
Then vertical distance corresponding to horizontal distance x is;
or,
which is parabolic in nature.
At point p, ,
so, resultant velocity v=
And angle made by velocity
Time of flight =
Range=u.t=u*