Friction
Friction
•It is an electromagnetic force playing between any two surfaces.
•It always acts opposite to direction of motion or opposite to direction of tending motion.
•It is independent of force applied and external factors.
•It depends on internal properties of body and regularity of plane.
•Mathematically, frictional force is directly proportional to Normal Reaction. i.e α R or =μR where μ is the coefficient of friction.
Types of friction
•Static Friction(μs): Opposing force which comes to play when a body tends to move on another.
-Limiting friction is the maximum value of frictional force.
•Dynamic Friction(μk): Opposing force which comes to play when a body move on another.
•Rolling Friction(μr): Opposing force which comes to playμ when a body rolls on another.
Related as,
Frictional force comparison on plane
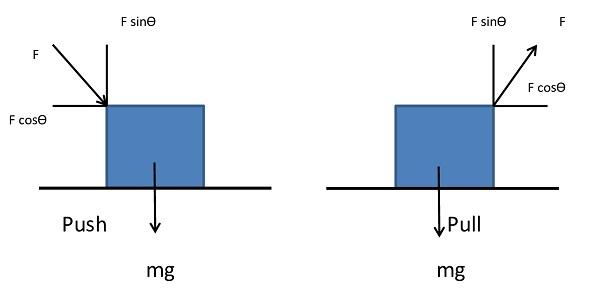
While pushing:
While pulling:
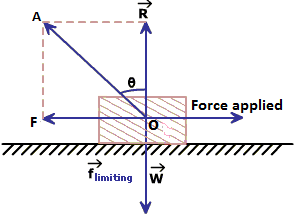
Angle of friction and angle of repose
•Angle of friction(): Angle made by frictional force with Normal reaction.
==μ
•Angle of repose(): Maximum angle in which an object can rest on inclined plane without sliding.
=
So, angle of friction=angle of repose= θ = α =
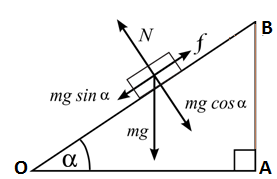
Minimum force to slide on inclined plane
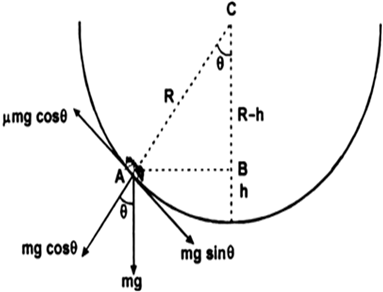
Maximum height an insect can crawl on bowl
Problems on chain
•A chain of length L is overhung from edge of horizontal table with its length x then μ=?
-1665984216371-aakhyaan.org-.png)
•Frictional force = weight of overhung for equilibirium.
So, or,
Ratio of overhung length is