Vectors and relative velocity
Vector
•Quantities which has both magnitude and direction and follow law of vector addition.
eg: Field strength, gradient of scalar, small length and area are always vectors.
•Note that, flux of vectors, potential of vectors etc. are always scalar.
•Unit vector: Whose magnitude is unity.
Tensor
•It is a quantity whose magnitude changes from direction to direction.
•Which is neither vector or scalar.
•Rank 1 is vector and rank 0 is scalar….(Matrices)
eg. stress, coefficient of viscocity, energy (However in classical mechanics it is expressed as scalar) etc.
Triangle law of vector addition
If two sides of a triangle completely represent two vectors both in magnitude and direction taken in same order, then the third side taken in opposite order represents the resultant of the two vectors both in magnitude and direction.
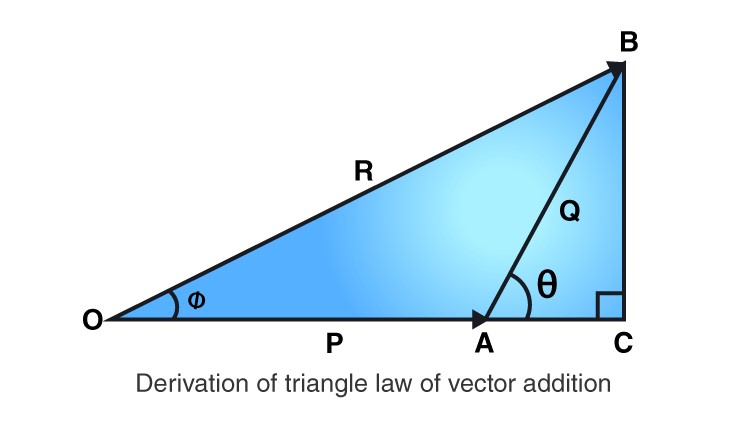
Here, where is the resultant.
Parallelogram law of vector addition
If two vectors acting simultaneously at a point are represented both in magnitude and direction by two adjacent sides of a parallelogram drawn from the point, then the diagonal of the parallelogram passing through that point represents the resultant both in magnitude and directions.
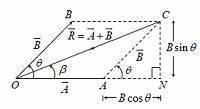
||=
=tan-1
Scalar product
Called as scalar product because the resultant is scalar.
Also called as dot product.
It is defined as =
Vector product
called as vector product because the resultant is vector.
also known as cross product.
-1665415804703.png)
It is defined as =
is the unit vector perpendicular to both and . so is also perpendicular to both and .
Difference of two vectors
•It’s the addition of with-where are any two vectors.
-1665416518206.png)
=
=
Angle of resultant with is given by
=
Relative velocity
It's the velocity of moving body with respect to another.
=(velocity of A with respect to B)
=(velocity of B with respect to A)
-1665417487351.png)
The direction of (velocity of A with respect to B) is shown in fig and given as
=
=
Direction ofwithis =
Relative velocity is added when bodies are moving towards each other and subtracted when approaching each other.
*If largest magnitude is less than or equal to sum of other magnitudes their resultant may be zero.
*Eg: Can the resultant of 10N,5N,6N be zero?
ANS: yes.
Because 5N,6N can give resultant of 10N at any angle calculated. Which when applied on opposite direction of force 10N, the resultant may be zero.
•If largest magnitude is greater than or equal to sum of other magnitudes their resultant can never be zero.
Eg. Can the resultant of 10N,5N,4N be zero?
Ans: No.
Because 5N,4N gives maximum resultant of9N at angle 0, Which when applied on opposite direction of force 10N, the resultant remains still 1N, which is not zero.
Vectors giving resultant zero
•Minimum number of collinear vectors giving resultant zero is 2.
•Minimum number of collinear vectors of unequal magnitude giving resultant zero is 3.
•Minimum number of coplanar vectors giving resultant zero is 3.
•Minimum number of non coplanar vectors giving resultant zero is 4.
Notes on Vector Calculations
•| | and || has range R, (a+b)≤R ≤(a-b).
•If ϴ=0°, then || = (a+b) =maximum and ||= (a-b) =minimum.
•If ϴ=90°, then || =| | = .
•If ϴ=180°, then || =n(a-b) or(b-a) and | | = (a+b).
•If ||=| |=Athen | | =2Acosand| | =2Asin