Elasticity
Elasticity
It is the property of a body by virtue of which it tends to regain its original shape and size when the deforming force is removed.
Perfectly elastic body: The body regains its original shape and size completely and instantaneously on the removal of the deforming force.
Perfectly plastic body: The body which does not regain its original configuration at all on the removal of deforming force, however small the deforming force may be.
Inter atomic force: The force which is responsible to hold together the atoms or molecules of a matter is called inter atomic force.
Stress: The restoring force per unit area of the body is called stress.
Its SI unit is and CGS unit is dyne cm-2.
Types of stress
a. Normal stress: If the deforming force is applied normally to the surface of a body, the applied force per unit area is called normal stress.
i. Tensile stress: If there is an increase in length or extension of the body in the direction of the force applied, the stress set up is called tensile stress.
ii. Compression stress: If there is a decrease in length of the wire or compression of the body due to the force applied, the stress set up is called compression stress.
b. Tangential stress or shearing stress: It is defined as the ratio of the force acting tangent to the surface to the area of the surface.
c. Bulk stress or volume stress or hydraulic stress
Strain: The ratio of the change in configuration (i.e. shape, length or volume) to the original configuration of the body is called strain.
Types of strain
i. Longitudinal strain
ii. Volumetric strain
iii. Shear strain
( if is small )
where is the angle through which the face of the body originally perpendicular to the fixed face is turned when it is under the shearing stress.
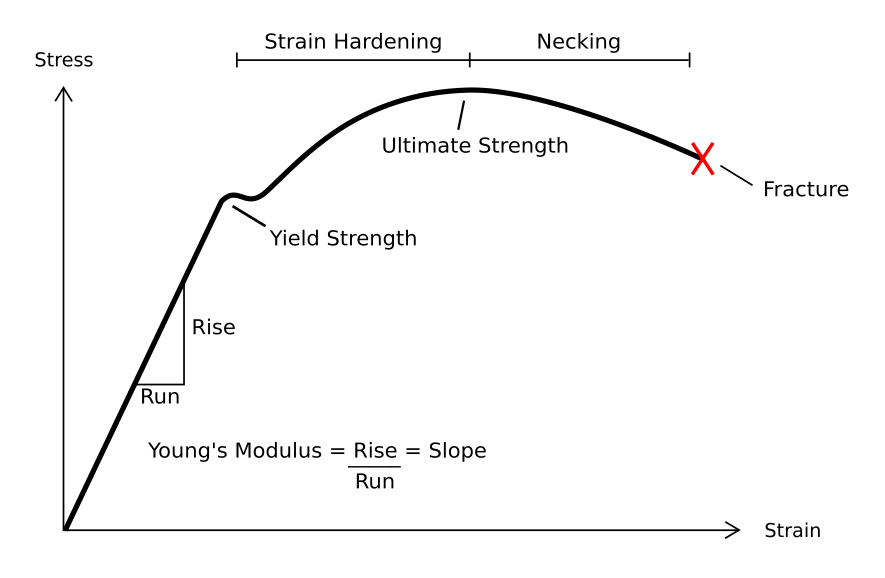
Elastic Limit
It is the upper limit of deforming force up to which if deforming force is removed, the body regains its original form completely and beyond which if deforming force is increased, the body loses its property of elasticity and gets permanently deformed.
Hooke's Law
Restoring force acting on elastic body is directly proportional to extension produce within elastic limit.
where k is force constant or spring constant.
Further it is modified by Young, which states ' the stress developed is directly proportional to the strain produced in a body.'
where E is the modulus of elasticity.
A graph between stress and strain for a ductile metal under tension
Types of Moduli of Elasticity
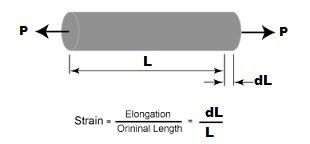
Young's modulus of elasticity,Y
It is defined as the ratio of normal stress to the longitudinal strain within the elastic limit.
Young's modulus ,
If the extension is produced by the load of mass m, then F=mg and area of cross section of the wire then
Bulk modulus of Elasticity,K
It is defined as the ratio of normal stress to the volumetric strain, within the elastic limit.
volumetric strain=
Normal stress=